Exploring the mod-$N$ Fibonacci sequence
Every math student will at some point in his life have encountered the famous Fibonacci sequence. This sequence, which I will denote by $F_n$, is defined by means of the recursive relation \[ F_n = F_{n - 2} + F_{n - 1} \] with starting values $F_0 = 0$ and $F_1 = 1$. The Fibonacci sequence can be analysed with some basic tools from real analysis and elementary number theory. Among other things, the $n$-th Fibonacci number may be found to have an explicit formula in terms of the golden ratio. The reader may perhaps also remember how the terms can be recovered from the shallow diagonals of Pascal’s triangle.
It might then come as a surprise that there are quite a number of open questions surrounding the Fibonacci sequence. In this post, I will outline one particularly fascinating source of open problems, which is the behaviour of the Fibonacci sequence modulo a fixed integer $N$, or equivalently, the Fibonacci sequence in the group $\mathbb{Z} / N \mathbb{Z}$.Note 1 There are many questions one can ask about this sequence, though I will confine myself mostly to just a single question, which is what we can say about the period of this sequence for varying $N$.
Searching online I came to find that this period, denoted $\pi(N)$, is called the $N$-th Pisano period. I will be using the term as well though I should confess that I hadn’t heard that term before. I’m also not aware of any mathematician named Pisano. That said, Fibonacci was from Pisa, so it may just be Fibonacci in linguistic disguise.
I will assume that the reader has some basic familiarity with abstract algebra and algebraic number theory.
Some values
Before diving into the theory, let’s do some computations to obtain some heuristics. The following simple Python script takes an integer $N$ as input and returns the period of the mod-$N$ Fibonacci sequence.
def Pisano(N):
"""Computes the period of the Fibonacci sequence modulo N."""
i0 = 1 #We start with F1 and F2
i1 = 1
count = 1
while (i0 != 0 or i1 != 1): #Proceed through the sequence until we find '0, 1'
i2 = (i0 + i1) % N
i0 = i1
i1 = i2
count += 1
return countLet’s compute the first 10,000 values and plot the results.
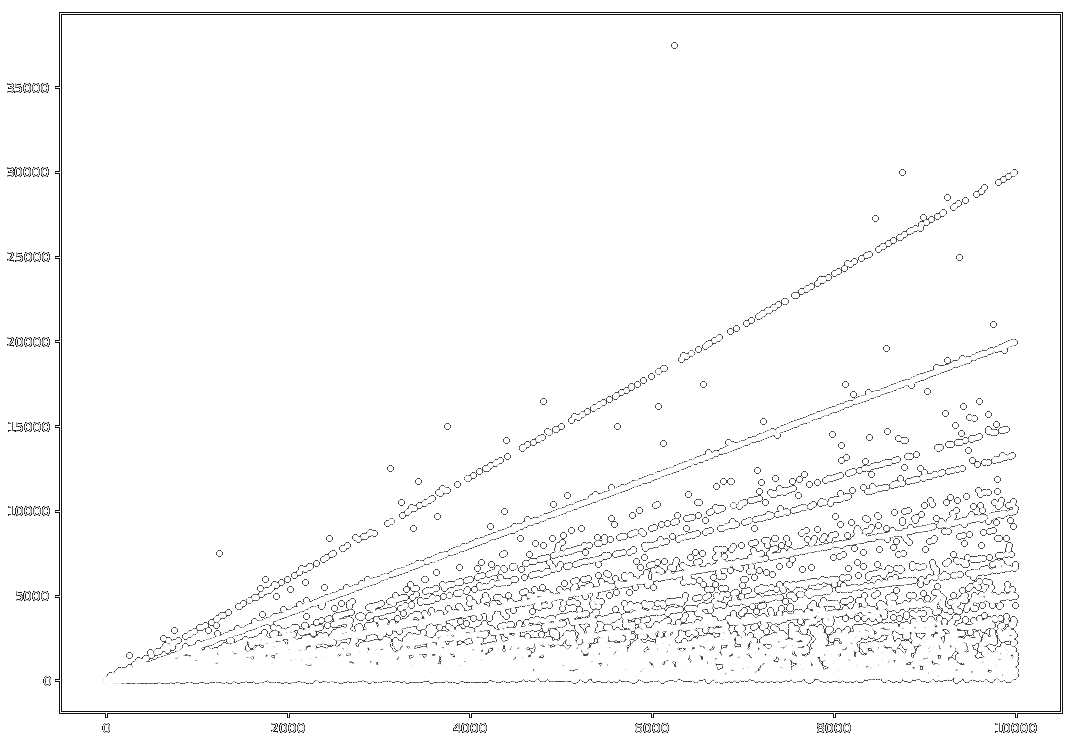
The first thing we immediately observe is these obvious lines appearing in our plot, of which the thickest seems to have slope $2$. Although not obvious from the plot, none of these lines are perfect; for instance, many $N$ have $\pi(N)$ almost but not exactly equal to $2N$. We also observe a rather strong outlier at $N \approx 6000$. This value turns out to be $N = 6250$ with $\pi(N) = 37\,500 = 6N$. Extending our plot would reveal that it doesn’t get any more extreme than this; indeed, we will show that $\pi(N) \leq 6N$.
Group-theoretic interpretation
The recurrence relation defining the Fibonacci sequence may be expressed in terms of matrices as \[\begin{pmatrix} F_{n + 1} & F_n \\ F_n & F_{n - 1} \end{pmatrix} = B^n\] where we have put \[B = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \text{.} \] As such, we find that we may interpret the periodicity of the mod-$N$ Fibonacci sequence is equal to the order of the element $B$ in the general linear group $\mathrm{GL}_2(\mathbb{Z}/N\mathbb{Z})$.
To obtain some more information from this perspective let us take a closer look at the groups of interest. We may as well begin with a little numerical investigation. To this end, let’s first make the following observation. If $N > 2$, then the determinant of $B$ is $-1$, and so its order must necessarily be even. In fact, we may as well look at the order of $B^2$, and then multiply everything by $2$. The advantage that this brings is that $B^2$ has determinant $+1$, so that it lives in the well-studied special linear group $\mathrm{SL}_2(\mathbb{Z}/N\mathbb{Z})$. This group is significantly smaller than $\mathrm{GL}_2(\mathbb{Z}/N\mathbb{Z})$, and is thus likely easier to handle with brute-force methods.
The computer algebra system GAP is equipped to handle special linear
groups; indeed we may load in our group as
G = SL(2,ZmodnZ(N)). Let’s brute-force some basic
numerical properties for these groups. In particular, we will enumerate
the possible orders of the elements in $G$. There is no built-in GAP
function to do this, so we do it by hand. We sigificantly save computing
time by noting that it suffices to compute the orders for
representatives of the conjugacy classes, which GAP is equipped to
handle. The following Python code can be run in SageMath, which has GAP
built into its library.
def possibleOrders(G):
"""Computes the possible orders of all elements in a group G."""
cc = gap.ConjugacyClasses(G)
orders = [gap.Order(gap.Representative(c)) for c in cc]
orders = sorted(set(orders))
return ordersBelow, we have listed the results of our computations for the first $20$ values of $N$. $|G|$ denotes the order of $G$; $c(G)$ denotes the number of conjugacy classes; $\exp(G)$ denotes the exponent of $G$.Note 2
| $N$ | $|G|$ | $c(G)$ | Possible orders | $\exp(G)$ | $\pi(N)$ |
|---|---|---|---|---|---|
| $1$ | $1$ | $1$ | $\{1\}$ | $1$ | $1$ |
| $2$ | $6$ | $3$ | $\{1, 2, 3\}$ | $6$ | $3$ |
| $3$ | $24$ | $7$ | $\{1, 2, 3, 4, 6\}$ | $12$ | $8$ |
| $4$ | $48$ | $10$ | $\{1, 2, 3, 4, 6\}$ | $12$ | $6$ |
| $5$ | $120$ | $9$ | $\{1, 2, 3, 4, 5, 6, 10\}$ | $60$ | $20$ |
| $6$ | $144$ | $21$ | $\{1, 2, 3, 4, 6, 12\}$ | $12$ | $24$ |
| $7$ | $336$ | $11$ | $\{1, 2, 3, 4, 6, 7, 8, 14\}$ | $168$ | $16$ |
| $8$ | $384$ | $30$ | $\{1, 2, 3, 4, 6, 8\}$ | $24$ | $12$ |
| $9$ | $648$ | $25$ | $\{1, 2, 3, 4, 6, 9, 12, 18\}$ | $36$ | $24$ |
| $10$ | $720$ | $27$ | $\{1, 2, 3, 4, 5, 6, 10, 12, 15, 30\}$ | $60$ | $60$ |
| $11$ | $1320$ | $15$ | $\{1, 2, 3, 4, 5, 6, 10, 11, 12, 22\}$ | $660$ | $10$ |
| $12$ | $1152$ | $70$ | $\{1, 2, 3, 4, 6, 12\}$ | $12$ | $24$ |
| $13$ | $2184$ | $17$ | $\{1, 2, 3, 4, 6, 7, 12, 13, 14, 26\}$ | $1092$ | $28$ |
| $14$ | $2016$ | $33$ | $\{1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 42\}$ | $168$ | $48$ |
| $15$ | $2880$ | $63$ | $\{1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30\}$ | $60$ | $40$ |
| $16$ | $3072$ | $76$ | $\{1, 2, 3, 4, 6, 8, 12, 16\}$ | $48$ | $24$ |
| $17$ | $4896$ | $21$ | $\{1, 2, 3, 4, 6, 8, 9, 16, 17, 18, 34\}$ | $2448$ | $36$ |
| $18$ | $3888$ | $75$ | $\{1, 2, 3, 4, 6, 9, 12, 18\}$ | $36$ | $24$ |
| $19$ | $6840$ | $23$ | $\{1, 2, 3, 4, 5, 6, 9, 10, 18, 19, 20, 38\}$ | $3420$ | $18$ |
| $20$ | $5760$ | $90$ | $\{1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30\}$ | $60$ | $60$ |
Some reverse searching in the OEIS reveals that these sequences have already been classified. The size, number of conjugacy classes, and exponent, are listed as sequences A000056, A065501, and A327569.
To me, one thing stands out in the data, which is that the possible orders of the elements are remarkably constrained. As it turns out, this is to be expected of matrix groups in general. In fact, if $R$ is a finite ring, then the maximal order of any element in $\mathrm{GL}_n(R)$ will be $|R|^n - 1$. Indeed we may consider the $R$-subalgebra of the matrix algebra $M_n(R)$ generated by $A$, which by Cayley–Hamilton will be at most $n$-dimensional and can thus consist of at most $|R|^n$ elements, of which all but one are nonzero.
For $\mathrm{SL}_2(\mathbb{Z}/N\mathbb{Z})$, I in fact make the stronger claim that the order of an element can be at most $3N$, and that this bound is achieved only when $N$ is of the form $2 \times 5^e$ for some exponent $e \geq 1$. Let’s try and prove the first part of the claim. We will first consider the case where $N$ is a prime $p$. The advantage that this brings is that $\mathbb{Z} / N \mathbb{Z}$ becomes a field, $\mathbb{F}_p$, allowing us to use tools from linear algebra.
Let us denote by $A$ a matrix in $\mathrm{SL}_2(\mathbb{Z})$, and write $\operatorname{ord}_N(A)$ for the order of $A$ in the group $\mathrm{SL}_2(\mathbb{Z}/N\mathbb{Z})$. Notice that, for $N$ greater than $2$, $\pi(N) = 2 \operatorname{ord}_N(B^2)$ where $B$ is the matrix we introduced earlier.
Lemma. Let $p$ be an odd prime. The possible orders of elements in $\mathrm{SL}_2(\mathbb{F}_p)$ are divisors of $p - 1$, $p + 1$, or $2p$.Note 3
Proof: Consider a matrix $A$ in $\mathrm{SL}_2(\mathbb{F}_p)$. Then $\operatorname{ord}_p(A)$ will depend on the diagonalisability properties of $A$, and so we shall distinguish between a few different cases. First off, suppose that $A$ is diagonalisable in $\mathbb{F}_p$. Then it has two eigenvalues in $\mathbb{F}_p^{\times} \cong C_{p - 1}$, so the order of $A$ will be divisible by $p - 1$.
If $A$ is not diagonalisable in $\mathbb{F}_p$, then it may still be diagonalisable in the algebraic closure $\overline{\mathbb{F}_p}$. As the minimal polynomial has degree at most $2$, its splitting will necessarily occur in the finite field $\mathbb{F}_{p^2}$. Moreover, the two eigenvalues $\lambda$ and $\mu$ must be Galois conjugate, and as such they are permuted by the Frobenius automorphism; concretely, $\lambda^p = \mu$ and $\mu^p = \lambda$. We may use this to prove that the orders of $\lambda$ and $\mu$ in $\mathbb{F}_{p^2}^{\times}$ must be a divisor of $p + 1$. To wit, $\lambda^{p + 1} = \lambda \lambda^p = \lambda \mu = 1$, where the last equality follows from the standing assumption that $A$ has determinant $1$. By symmetry, the same proof applies to $\mu$. We conclude that the order of $A$ is divisible by $p + 1$.
Finally, assume that $A$ is not diagonalisable in $\overline{\mathbb{F}_p}$. Then the minimal polynomial of $A$ fails to split into distinct linear factors, and $A$ must have a single eigenvalue $\lambda$. Since $\lambda^2 = \det(A) = 1$, $\lambda$ must be $\pm 1$. It follows that the minimal polynomial of $A^2$ will be $(x - 1)^2$, hence the minimal polynomial of $A - I$ will be $x^2$. Minimal polynomials detect nilpotence, so $(A^2 - I)^2 = O$. We may thus write $A^2 = (N + I)$ where $N^2 = O$. Now take its $p$-th power and apply the binomial expansion to find that $A^{2p} = (N + I)^p = I$. We conclude that $A$ must have order divisible by $2p$. ∎
To pass from prime numbers to more general $N$, we first observe that by the Chinese remainder theorem $\operatorname{ord}_{(\,\cdot\,)}(A)$ satisfies the multiplicativity property that $\operatorname{ord}_{N_1 N_2}(A)$ equals the least common multiple of $\operatorname{ord}_{N_1}(A)$ and $\operatorname{ord}_{N_2}(A)$ whenever $N_1$ and $N_2$ are coprime. Thus, we may as well restrict our attention to the case where $N$ is a prime power $p^k$, where we have the following.
Lemma. Let $p$ be a prime number. Then $\operatorname{ord}_{p^k}(A)$ divides $p^{k-1} \operatorname{ord}_{p}(A)$.
Proof: In fact, if $p$ divides $N$, then $\operatorname{ord}_{pN}(A)$ divides $p \operatorname{ord}_{N}(A)$. Indeed if we consider $A$ in $\mathrm{SL}_2(\mathbb{Z}/pN\mathbb{Z})$ then $A^{\operatorname{ord}_N(A)}$ will be in the kernel of the reduction mod $N$, and as such $A^{\operatorname{ord}_N(A)}$ can be written as $I + N B$ for some matrix $B$. In particular, $A^{p \operatorname{ord}_N(A)}$ becomes $(I + NB)^{p}$, which by the binomial expansion may be seen to reduce to $I$ modulo $pN$. ∎
We will briefly revisit this lemma in a later section. For our current purposes, we have enough information to prove the following result:
Theorem. For any matrix $A$ and any integer $N$, $\operatorname{ord}_N(A) \leq 3N$, hence $\pi(N) \leq 6N$.
Proof: First consider the case that $N$ is odd. Write $N = p_1^{e_1}\cdots p_r^{e_r}$. Then we have \[\operatorname{ord}_N(A) = \operatorname{lcm}\!\big(\!\operatorname{ord}_{p_1^{e_1}}(A),\ldots,\operatorname{ord}_{p_r^{e_r}}(A)\big)\text{.} \] From our previous results we know that each $\operatorname{ord}_{p_i^{e_i}}(A)$ is a divisor of $p_i^{e_i - 1}(p_i - 1)$, $p_i^{e_i - 1}(p_i + 1)$, or $2p_i^{e_i}$, all of which are even. As such, \[\operatorname{lcm}\!\big(\!\operatorname{ord}_{p_1^{e_1}}(A),\ldots,\operatorname{ord}_{p_r^{e_r}}(A)\big) \leq 2 \prod_{i=1}^{r} p_i^{e_i} = 2N \text{.} \] Now let’s consider the case that $N$ is even. Decompose $N$ as $2^e N'$ where now $N'$ is odd. Then \[ \operatorname{ord}_N(A) = \operatorname{lcm}\!\big(\!\operatorname{ord}_{2^e}(A),\operatorname{ord}_{N'}(A)\big)\text{.} \] By the discussion above, $\operatorname{ord}_{N'}(A) \leq 2N$. Moreover, by the previous lemma, $\operatorname{ord}_{2^e}(A)$ is a divisor of $2^{e-1} \operatorname{ord}_{2}(A)$. By looking at our table all elements in $\mathrm{SL}_2(\mathbb{Z}/2\mathbb{Z})$ have orders $1$, $2$ or $3$, so in any case $\operatorname{ord}_{2^e}(A) \leq 2^{e-1} \times 3$. Together, \[ \operatorname{ord}_N(A) \leq 2^{e-1} \times 3 \times 2N' = 3N \text{,} \] as desired. ∎
It is tempting to ask when this bound is sharp. That is, for which $N$ does there exist a matrix $A$ in $\mathrm{SL}_2(\mathbb{Z}/N\mathbb{Z})$ of order $3N$? Moreover, for which $N$ does our specific choice of $A$, \[ A = B^2 = \begin{pmatrix} 2 & 1 \\ 1 & 0 \end{pmatrix} \text{,} \] have order $3N$? Numerical calculations suggest to me that both of these questions have a structured answer. The matrix $B^2$ appears to have order $3N$ if and only if $N = 2 \times 5^e$ for some exponent $e \geq 1$. But there are other $N$ for which other matrices of order $3N$ can be found; looking at our table shows that $N = 14$ is already an example. In fact, I would conjecture that $\mathrm{SL}_2(\mathbb{Z} / N \mathbb{Z})$ has an element of order $3N$ if and only if $N \equiv 2,10 \,(\mathrm{mod}\,12)$. I do not yet know how to prove either of these claims.
Number-theoretic interpretation
There is an explicit formula for the $n$-th Fibonacci number involving the golden ratio $\varphi$: \[ F_n = \frac{\varphi^n - \overline{\varphi}^n}{\varphi - \overline{\varphi}}\text{,} \] where $\overline{\varphi}$ denotes the Galois conjugate of $\varphi$; that is, $\varphi = (1 + \sqrt{5}) / 2$ and $\overline{\varphi} = (1 - \sqrt{5}) / 2$. The straightforward proof of this identity carries over verbatim to other rings provided that the golden ratio makes sense in that ring. What if the ring is $\mathbb{Z} / N \mathbb{Z}$?
If we consider the ring $\mathbb{Z} / N \mathbb{Z}$, we will want the number $N$ to be odd, since otherwise $2$ becomes a zero divisor, and thus dividing by $2$ doesn’t make sense. In turn, for odd $N$, it’s not always the case that $\sqrt{5}$ exists in the ring. Put in other terms, it is not true that $5$ is a square modulo $N$ for all $N$. However, in these cases we may simply adjoin an abstract element $\sqrt{5}$ to the ring. For what it’s worth, the $N$ for which $5$ is a square mod $N$ can be classified:
Lemma. $5$ is a square modulo $N$ if and only if in the prime decomposition $N = 2^e p_1^{e_1} \cdots p_r^{e_r}$ we have $e \leq 2$ and $p_1,\ldots,p_r\equiv 1,4\,(\mathrm{mod}\,5)$.
Proof sketch: Reduce to the case of prime powers using the Chinese remainder theorem and then further to the case of prime numbers using Hensel’s lemma. The case where $N$ is prime follows from the standard theory of Legendre symbols. ∎
Just as in the previous section, the situation becomes simpler to analyse when we assume that $N$ is a prime. In that case, the ring $\mathbb{Z} / N \mathbb{Z}$ becomes a field $\mathbb{F}_p$, which gives us some additional flexibility.
Lemma. Let $p$ be a prime not equal to $2$ or $5$. Let $k$ denote the field $\mathbb{F}_p(\sqrt{5})$, which is $\mathbb{F}_p$ if $p \equiv 1,4\,(\mathrm{mod}\,5)$ and $\mathbb{F}_{p^2}$ otherwise. Then the $p$-th Pisano period is equal to the order of $\varphi$ in the unit group $k^{\times}$.
If you prefer thinking about field extensions, the lemma can be stated more elegantly by saying that $\pi(p)$ is the multiplicative order of the roots of the polynomial $x^2 - x - 1$ in $\mathbb{F}_{p^2}$.
Proof: Suppose that $\varphi^c = 1$ for some $c$. Then $F_{n + c} = F_n$ for all $n$ since \[\begin{split} \frac{\varphi^{n + c}- \overline{\varphi}^{n + c}}{\varphi - \overline{\varphi}} &= \frac{\varphi^{n} \varphi^{c}- \overline{\varphi}^{n} \overline{\varphi}^c}{\varphi - \overline{\varphi}} \\ &= \frac{\varphi^n - \overline{\varphi}^n}{\varphi - \overline{\varphi}} \text{.} \end{split} \] Conversely if $c$ is a number such that $F_{n + c} = F_n$ for all $n$ then we claim that $\varphi^c = 1$. To prove this, we start with the same equality \[ \frac{\varphi^{n + c}- \overline{\varphi}^{n + c}}{\varphi - \overline{\varphi}} = \frac{\varphi^n - \overline{\varphi}^n}{\varphi - \overline{\varphi}} \] and we use the fact that we’re working in a field to rewrite this into \[ \varphi^n(\varphi^{c} - 1) = \overline{\varphi}^n(\overline{\varphi}^{c} - 1) \text{.} \] If $\varphi^c \neq 1$ then we could rewrite this further into \[ \bigg(\frac{\varphi}{\overline{\varphi}}\bigg)^n = \frac{\overline{\varphi}^c - 1}{\varphi^{c} - 1} \text{.} \] Clearly the right-hand side is constant for different $n$, which would imply that the same is true for the left-hand side, forcing an equality $\varphi = \overline{\varphi}$, and thus $\sqrt{5} = 0$, which is absurd. ∎
A consequence of this lemma is that if $p \equiv 1,4\,(\mathrm{mod}\,5)$ then $\pi(p)$ must be a divisor of $p - 1$. This bound is significantly stronger than the one obtained from group theory, and as before it’d be a reasonable question to ask whether it is sharp. As it happens, it is an open question whether there are infinitely many $p$ such that $\pi(p) = p - 1$. In fact, it’s a special case of a famous conjecture of Artin.
Artin’s conjecture on primitive roots states the following question. If $a$ is an integer which is neither a perfect square nor $-1$, then are there infinitely prime numbers $p$ for which the multiplicative order of $a$ is maximal, i.e. equal to $p - 1$? This conjecture is open for all $a$.
There’s an obvious generalisation of Artin’s conjecture to more general number fields. Let $K$ denote a number field, and suppose that $a$ is an integer in $\mathcal{O}_K$ which is neither a root of unity nor a perfect power. Then there are expected to be infinitely many prime ideals $\mathfrak{p}$ such that $a$ has maximal multiplicative order in the residue field $\mathcal{O}_K / \mathfrak{p}$. Our question about maximal Pisano periods would be the special case where $K = \mathbb{Q}(\sqrt{5})$ and $a = (1+\sqrt{5}) / 2$.
It appears to be known that both Artin’s conjecture and its generalisation are a consequence of the generalised Riemann hypothesis.
A trivial lower bound
We have concerned ourselves much with upper bounds for Pisano periods, but what about lower bounds? This question is arguably less interesting. There’s an obvious lower bound which follows from the fact that if $N$ is very large, it takes a while for $F_n$ to reach $N$. In fact, as $F_n$ grows exponentially, we accordingly expect a logarithmic lower bound. It is natural to ask if this bound can be improved, but a swift glance at our graph of the first 10,000 values indicates that there are many large $N$ with small $\pi(N)$, so it seems unlikely that there is much more to be said.
The mystery of Wall–Sun–Sun primes
In our study of Pisano periods, we learned that it suffices to look the case where $N$ is a prime power. However, we often confined our attention to the case where $N$ is a prime, sweeping under the rug the precise relation between the period of a prime and that of its powers.
We had proved through elementary means that $\pi(p^k)$ divides $p^{k-1} \pi(p)$. Numerical calculations in fact suggests that we often have an equality $\pi(p^k) = p^{k-1} \pi(p)$. Surprisingly, not a single prime is known for which this equality fails, yet it is suspected that there are infinitely many of them.
To understand this, let’s consider the special case $k = 2$. The so-called Wall–Sun–Sun primesNote 4 are prime numbers $p$ such that $\pi(p^2) = \pi(p)$ instead of the usual $\pi(p^2) = p \,\pi(p)$. No Wall–Sun–Sun primes are known to exist; in fact, we have ruled out the existence of any Wall–Sun–Sun primes smaller than $10^{15}$. Nonetheless, there’s a simple heuristic reason to believe that there are infinitely many of them:Note 5
Statistically speaking, there’s roughly a one in $p$ chance that the multiplicative order of an element in $\mathbb{Z}/p^2\mathbb{Z}[\sqrt{5}]$ is the same as the multiplicative order of its reduction modulo $p$. As such, the expected number of Wall–Sun–Sun primes in the range $[a,b]$ is approximately \[ \sum_{x \leq p \leq y} \frac{1}{p} \approx \log \log y - \log \log x \text{.} \] In particular, the expected number of Wall–Sun–Sun primes below $10^{15}$ is only around $3$, which is not particularly far from the $0$ that we have found so far.
Footnotes
- Algebraists may find this point of view enticing as it suggests a generalisation to arbitrary groups. If $G$ is a group (say a finite group or a Lie group) and $x$ and $y$ are elements, we may define a Fibonacci sequence $F_n$ by setting $F_0 = x$, $F_1 = y$, and $F_n = F_{n-2} F_{n-1}$. What can we say about this sequence in general? I haven’t given this question a thought yet, but I’m sure there’s many interesting things waiting to be found.
-
The group exponent can be obtained as the least common multiple of the
elements’ orders; however, GAP has a built-in function
Exponent()which appears to be significantly faster. - I invite the reader to ask himself which parts of the proof fail when we pass to bigger matrices or to the general linear group. As a first step, can you get concrete statements about the orders of elements in $\mathrm{SL}_3(\mathbb{F}_p)$ or $\mathrm{GL}_2(\mathbb{F}_p)$? Also, what can you say about the converse statement? That is, do all divisors of $p - 1$, $p + 1$ and $2p$ arise as the order of some element in $\mathrm{SL}_2(\mathbb{F}_p)$?
- The two Sun’s seem to be twins.
- This is the same heuristic that is commonly used to conjecture that there are infinitely many Wilson primes.