Some elementary problems solved with elliptic curves

Quite recently I had the pleasure of teaching a course on elliptic curves, with a particular focus on arithmetic phenomena. Towards the end of the course I found myself having to give a lecture with no particular scheduled topic, so I opted to use that time to apply the theory we built up thus far to tackle some elementary puzzles.

Cannonball problem

The famous cannonball problem asks the following question. I have a collection of cannonballs, arranged on a square grid which I will suggestively say is of size $y$. For which $y$ can I stack my cannonballs into a square pyramid? Mathematically, what we are asking is: For which $y$ is the number $y^2$ square pyramidal?

Let’s assume that the hypothetical square pyramid is of height $x$. Then the pyramid consists of a total of \[ f(x) = \sum_{i = 0}^{x} i^2 \] cannonballs. Since $f(x) - f(x - 1) = x^2$, we expect $f(x)$ to be expressible as a cubic equation, say $ax^3 + bx^2 + cx + d$ for some $a$, $b$, $c$ and $d$. The volume of a height-$x$ square pyramid is $x^3 / 3$ so by asymptotic reasoning we know that $a = 1/3$. A height-$0$ square pyramid has $f(0) = 0$ cannonballs, so $d = 0$. Likewise, $f(1) = 1$ and $f(2) = 5$, which yields the equations \[ \frac{1}{3} + b + c = 1 \qquad \text{and} \qquad \frac{8}{3} + 4b + 2c = 5 \text{.} \] Linear algebra (or the art of squinting) lets you see that $b = 1/2$ and $c = 1/6$. The validity of this equation can alternatively checked by induction.

By this point, we understand that solutions to the cannonball problem correspond to integral points on the elliptic curve defined by the equation \[ y^2 = \frac{1}{3} x^3 + \frac{1}{2} x^2 + \frac{1}{6} x \text{.} \] For convenience, we would like to express this elliptic curve in Weierstrass form. (This is not quite the case yet, due to the nontrivial coefficient in front of $x^3$.) However, care must be taken when doing this: unlike rational points, integral points are not invariant under isomorphism! An easy way to see this is by noting that a substitution as simple as $x \mapsto x + 1/2$ moves the $x$-coordinate by $1/2$, so any point which initially had integral $x$-coordinate now fails to do so.

If we make the substitution $X = 12x + 6$ and $Y = 72y$, then these new variables satisfy the equation \[ Y^2 = X^3 - 36X \text{,} \] which is an equation in (short) Weierstass form. Moreover, any integral solution to our original equation yields an integral solution to our new equation. (The converse is false, but this is not of any concern to us.) What are the integral points of this new equation?

By a famous theorem of Siegel, an elliptic curve will have finitely many integral points. This theorem is nonconstructive in that it does not indicate precisely how many points there will be. However, assuming that you know the generators of the Mordell–Weil group of your elliptic curve, then there are effective procedures to find all integral points.^{Note 1} The computer algebra system Sage has built-in algorithms for finding integral points on an elliptic curve:

E = EllipticCurve([-36, 0])
E.integral_points()

[(-6 : 0 : 1),
 (-3 : 9 : 1),
 (-2 : 8 : 1),
 (0 : 0 : 1),
 (6 : 0 : 1),
 (12 : 36 : 1),
 (18 : 72 : 1),
 (294 : 5040 : 1)]

In order for these integral points to correspond to integral points on our original equation, we want the $Y$-coordinate to be divisible by $72$. This yields only three points of interest: $(0, 0)$, $(18, 72)$, and $(294, 5040)$. Solving for $x$ and $y$, they give rise to integral solutions $(0, 0)$, $(1, 1)$ and $(24, 70)$ for our original equation.

The first two of these are not surprising; a $0 \times 0$ grid of cannonballs can indeed be rearranged into a height-$0$ square pyramid, and likewise for a $1 \times 1$ grid. But what about the last solution? It suggests that $70^2$ is square pyramidal, and indeed a direct computation will show you that \[ 70^2 = 1^2 + 2^2 + \cdots + 24^2 \text{.} \] That’s quite a striking numerical coincidence,^{Note 2} but it is equally striking that there are no further solutions beyond this point.

The Fermat curve

Fix an integer $n$. What are the rational solutions to the Diophantine equation $u^3 + v^3 = n$? After homogenising, this equation defines a curve in $\mathbb{P}^2$. In fact, this curve is elliptic, though perhaps not obviously so.^{Note 3} However, after performing the rather striking substitution \[ x = 12 n \frac{1}{u + v} \qquad \text{and} \qquad y = 36 n \frac{u - v}{u + v}\] we find the equation \[ y^2 = x^3 - 432 n^2 \text{,} \] which obviously defines an elliptic curve in Weierstrass form. To get back to $u$ and $v$, simply compute \[ u = \frac{36 n + y}{6x} \qquad \text{and} \qquad v = \frac{36n - y}{6x} \text{.} \] We can let Sage try and compute the rank and torsion subgroup of the rational points of this elliptic curve, and see what that gets us. Let’s start off with the case $n = 1$.

E = EllipticCurve([0, -432])
E.rank(); E.torsion_points()

0
[(0 : 1 : 0), (12 : -36 : 1), (12 : 36 : 1)]

Converting back to $u$- and $v$-coordinates we find that the only solutions to our equation are $(u,v) = (1,0)$ and $(u,v) = (0,1)$. This is not particularly surprising; indeed there are numerous proofs that the homogenised equation $u^3 + v^3 = w^3$ has no nontrivial integer solutions. But let’s consider some larger $n$ instead.

for n in range(1, 11):
    E = EllipticCurve([0, -432 * n**2])
    print("If n is", n, "then the rank is", E.rank())

If n is 1 then the rank is 0
If n is 2 then the rank is 0
If n is 3 then the rank is 0
If n is 4 then the rank is 0
If n is 5 then the rank is 0
If n is 6 then the rank is 1
If n is 7 then the rank is 1
If n is 8 then the rank is 0
If n is 9 then the rank is 1
If n is 10 then the rank is 0

What this tells us is that the equation $u^3 + v^3 = n$ has finitely many solutions when $n = 1,2,3,4,5$ (and in fact by examining the torsion points it’s easily observed that all these solutions are trivial) but once we reach $n = 6$ suddenly we find ourselves with an infinite family of solutions! Let’s examine these solutions in more detail. We can ask Sage for a torsionfree generator, and it will give us the point $P = (28,80)$, corresponding to a solution $(u,v) = (37/21, 17/21)$, and indeed a direct computation shows you that \[ 37^3 + 17^3 = 6 \times 21^3 \text{.} \] If we ask Sage to compute $2P$, it will return the point $(16009/100, -2021723/1000)$, corresponding to $(u,v) = (-1805723/960540, 2237723/960540)$, and indeed, \[ -1805723^3 + 2237723^3 = 6 \times 960540^3 \text{.} \] It goes without saying that larger multiples of $P$ result in more complicated solutions to our equation.

It’s reasonable to ask how the ranks develop as $n$ gets larger and larger. Unfortunately, Sage will give up at a certain point, because the standard algorithms invoked by Sage are not guaranteed to work, and tend to fail if the curve becomes too complicated. Sage offers you the option to instead use algorithms whose correctness is conjectural, but let’s not go through that, as others have surely done the work for us. We simply search the first couple of terms in the OEIS and see what we find. Lo and behold, we find that the sequence has been catalogued under A060838, which in turn gives us a reference to the ranks for the first $10\,000$ values of $n$. Curiously, the rank never manages to exceed $3$.

An infamous Facebook puzzle

As a final application, let’s take a look at this rather infamous ‘Facebook puzzle’, which many working mathematicians will certainly have seen before.

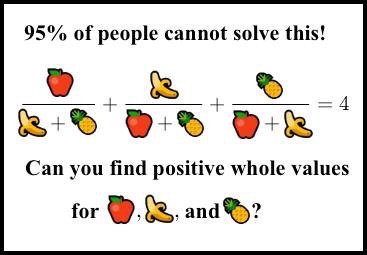
For typographical ease, let’s convert the apple, banana and pineapple into $a$, $b$, and $c$ respectively so as to obtain the equation \[ \frac{a}{b + c} + \frac{b}{c + a} + \frac{c}{a + b} = 4 \qquad \text{with} \qquad a,b,c \in \mathbb{Z}_{\geq 0} \text{.} \] The equation is homogeneous. This means that it suffices to find a solution in $\mathbb{Q}_{\geq 0}$, since we can just clear denominators afterwards. Moreover, it means that the equation defines a curve in $\mathbb{P}^2$. Although perhaps not obvious, this curve is in fact elliptic.^{Note 3} As before, a nontrivial substitution will let us see this more clearly. If we perform the substitution \[ x = -28 \frac{a + b + 2c}{6a + 6b - c} \qquad \text{and} \qquad y = 364 \frac{a - b}{6a + 6b - c} \text{,} \] then $x$ and $y$ will satisfy the Weierstrass equation \[ y^2 = x^3 + 109 x^2 + 224x \text{.}\] (It may strike you that we only have two variables rather than three — but remember that the original equation was homogeneous, so the third variable is a bit of a red herring.) Sage tells us that this is a curve of rank $1$, with torsion subgroup $\mathbb{Z}/6$. Thus, there are infinitely many rational points on our curve, and any of these points can be converted into a rational solution to our original equation by using the substitutions \[ (a,b,c) = \bigg( \frac{56 - x + y}{56 - 14x}, \frac{56 - x - y}{56 - 14x}, \frac{-28 - 6x}{28 - 7x}\bigg) \text{.} \] However, we caution that we specifically look for solutions for which $a$, $b$ and $c$ are positive.

We propose the following strategy to find an appropriate solution to our original equation: Starting with a choice of generator $P$ of the torsionfree component, compute the coordinates of $nP$ for $n = 1,2,3,\ldots$, convert these into a solution $(a,b,c)$, and check their signs. If all signs are positive, then we are done; if not, we move on to the next point.

You may wonder why we aren’t involving the torsion component into our search. As it happens, the torsion component cannot introduce any interesting new solutions: the $\mathbb{Z}/6$-component is merely a reflection of the intrinsic $\Sigma_3$-symmetry of the original equation, so adding the torsion point will simply permute the coordinates $(a,b,c)$.

E = EllipticCurve([0, 109, 0, 224, 0])
P = E.gens()[0]; Q = P
while True:
    x = Q[0]
    y = Q[1]
    a = (56 - x + y) / (56 - 14*x)
    b = (56 - x - y) / (56 - 14*x)
    c = (-28 - 6*x) / (28 - 7*x)
    if (a > 0) and (b > 0) and (c > 0):
        print(a, b, c)
        break
    Q += P

652194680638776317370751188686261401138670498641722947/826345176768069653846031682295795260307016241032351542
72627067629030455550043880234643101653454184810448427/385489402115598358968822193146517732601759618776822382
18811002229321433251069036843190834369329875858835562/841819787025663175191882291647234536827567920526661363

Without much effort, Sage finds a solution to our original equation! We can use Sympy to verify that this indeed produces an exact solution to our equation:

from sympy import Rational
a = Rational(652194680638776317370751188686261401138670498641722947, 826345176768069653846031682295795260307016241032351542)
b = Rational(72627067629030455550043880234643101653454184810448427, 385489402115598358968822193146517732601759618776822382)
c = Rational(18811002229321433251069036843190834369329875858835562, 841819787025663175191882291647234536827567920526661363)
out = a / (b + c) + b / (c + a) + c / (a + b)
print(out)

Footnotes

These procedures typically involve quite a bit of nontrivial height theory, and is beyond the scope of our discussion.
Incidentally, the construction of the Leech lattice strongly relies on this numerical coincidence.
It raises the question whether there’s a recognition principle for when a curve is elliptic. Surely such a principle exists; after all, elliptic curves are just curves of genus $1$ (with specified basepoint), and the genus is relatively easily computable.